Тогда тебе сюда: https://vk.cc/5OpAGz
понедельник, 7 ноября 2016 г.
пятница, 29 января 2016 г.
вторник, 12 января 2016 г.
ТВиМС экзамен (варианты прошлого года с решением)
Билет 2
ЗАДАЧА 3
По каналу связи передается 10 знаков. Вероятность искажения знака равно 0,2. Найти вероятность того, что будет искажено не более одного знака. Смотреть решение...ЗАДАЧА 4
Дана плотность распределения случайной величины e system{cx^2, 0 меньше или равно x меньше или равно 3; 0, x<0 data-blogger-escaped-x="">3}Найти константу c, функцию распределения F(x) и математическое ожидание m. Смотреть решение...
Билет 17
ЗАДАЧА 3
Три стрелка производят по одному выстрелу по мишени. Вероятности их попаданий соответственно равны 0.7 (1-ый стрелок), 0,8 (2-ой стрелок) и 0,9 (3-ий стрелок). Какова вероятность того, что в мишень попал 1-ый стрелок, если после выстрелов в мишени обнаружена одна пробоина.Смотреть решение...
ЗАДАЧА 4
Случайная величина e задана своим рядом распределения:Найти функцию распределения случайной величины n = 2e+1, ее математическое ожидание и дисперсию.
Смотреть решение...
ЗАДАЧА 5
Случайные величины X и Y имеют совместную плотность распределения. Найти константу c а также математическое ожидание случайной величины Z=X^2Y^2.Смотреть решение...
Билет 18
ЗАДАЧА 3
Найти вероятность того, что переданный по каналу связи и принятый приемником сигнал будет принят с ошибками, если вероятность искажения сигнала этим каналом равна 0,4, а вероятность искажения этим приемником равна 0,3. Смотреть решение...ЗАДАЧА 4
Плотность распределения вероятности f(x) задана выражением: system{Cx^3, 0 меньше или равно x меньше или равно 1; 0, x<0 data-blogger-escaped-x="">1}Найти: а) константу C; б) дисперсию случайной величины e+1 Смотреть решение...
ТВиМС кр3 с решением
Вариант 8
ЗАДАЧА 1
Стрелок производит стрельбу по мишени до первого попадания с вероятностью попадания p. Стрелку было выдано 4 патрона. Случайная величиная X - число использованных стрелком патронов. Найти ряд распределения и функцию распределения случайно величины X, ее математическое ожидание и дисперсию. Смотреть решение...ЗАДАЧА 2
Непрерывная случайная величина X задана плотностью распределения вероятностей. Найти значение постоянная a, функцию распределения и математическое ожидание. Смотреть решение...ЗАДАЧА 3
Найти константу с, законы распределения случайных величин X и Y, совместную функцию распределения, mx, my, проверить их независимость. Смотреть решение...ЗАДАЧА 4
Совместное распределение случайных величин X и Y задано плотностью распределения вероятностей. Найти константу с, плотности распределения и функции распределения с.в. X и Y, проверить их независимость, mx, my. Смотреть решение...ЗАДАЧА 5
Случайная величина X распределена по показательному закону с параметром лямбда. Найти плотность распределения вероятностей и математическое ожидание случайной величины U=1-e^(-лямбда*x)Смотреть решение...
Вариант 21
ЗАДАЧА 1
Устройство состоит из 4 независимо работающих элементов. Вероятности отказов каждого из элементов одинаковы и равны p=0,1. Случайная величина X - число отказавших элементов. Найти ряд распределения и функцию распределения случайной величины X, ее математическое ожидание и дисперсию. Смотреть решение...ЗАДАЧА 3
Найти константу с, одномерные законы распределения случайных величин X и У, совместную функцию распределения, M(X), M(Y), проверить их независимость: Смотреть решение...ЗАДАЧА 6
Случайные величины X и У независимы и распределены по следующим законам (таблицы). Найти ряд распределения, функцию распределения и математическое ожидание случайной величины Z=X^2+Y^2 Смотреть решение...понедельник, 11 января 2016 г.
Центральная предельная теорема. Примеры.
Мы будем называть следующее утверждение «ЦПТ Ляпунова(1)», но сформулируем и докажем теорему Ляпунова только в частном случае — для последовательности независимых и одинаково распределённых случайных величин. Как и ранее, через  обозначена сумма первых
обозначена сумма первых  случайных величин в последовательности:
случайных величин в последовательности:  .
.
Теорема 37 (ЦПТ Ляпунова). Пусть  — независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией:
— независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией:  . Тогда имеет место слабая сходимость
. Тогда имеет место слабая сходимость

последовательности «центрированных и нормированных» сумм случайных величин к стандартному нормальному распределению.
Пользуясь определением и свойствами слабой сходимости, и заметив, что функция распределения  любого нормального закона непрерывна всюду на
любого нормального закона непрерывна всюду на  (почему?), утверждение ЦПТ можно сформулировать любым из следующих способов:
(почему?), утверждение ЦПТ можно сформулировать любым из следующих способов:
Следствие 20. Пусть  — независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией. Тогда выполнены утверждения:
— независимые и одинаково распределённые случайные величины с конечной и ненулевой дисперсией. Тогда выполнены утверждения:
- а)
- для любых вещественных
при
имеет место сходимость
- б)
- если
— произвольная случайная величина со стандартным нормальным распределением, то
Замечание 27. Еще раз напомним, что функция распределения стандартного нормального закона ищется либо по соответствующей таблице в справочнике, либо с помощью какого-либо программного обеспечения, но никак не путем нахождения первообразной.
Мы докажем ЦПТ и ЗБЧ в форме Хинчина чуть позднее. Нам потребуется для этого познакомиться с мощным математическим инструментом, который в математике обычно называют «преобразованиями Фурье», а в теории вероятностей — «характеристическими функциями».
ТВиМС вопросы к экзамену 2016
6.
Предельные теоремы в схеме Бернулли. Локазьная и интегральная предельнаятеоремы Муавра-Лапласа. Теорема Пуассона. Примеры.
7.
Одномерные случайные величины. Функция и плотность распределениявероятностей и их свойства. Примеры.
12.
Системы случайных величин. Функция распределения вероятностей системы двухслучайных величин (двумерного случайного вектора), се свойства. Примеры.
28.
Интервальное (доверительное) оценивание. Доверительное оцениваниепараметров нормального распределения в одновыборочной совокупности.Доверительный интервал для вероятности в биномиальном распределении.
Простая линейная регрессия. Оценки параметров. Проверка значимости регрессии. Примеры.
Простая линейная регрессия.
Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.
Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.
Регрессионная модель
 ,
,
где  — параметры модели,
— параметры модели,  — случайная ошибка модели, называется линейной регрессией, если функция регрессии
— случайная ошибка модели, называется линейной регрессией, если функция регрессии  имеет вид
имеет вид
 — параметры модели,
— параметры модели,  — случайная ошибка модели, называется линейной регрессией, если функция регрессии
— случайная ошибка модели, называется линейной регрессией, если функция регрессии  имеет вид
имеет вид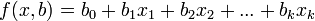 ,
,
где  — параметры (коэффициенты) регрессии,
— параметры (коэффициенты) регрессии,  — регрессоры (факторы модели), k — количество факторов модели.
— регрессоры (факторы модели), k — количество факторов модели.
 — параметры (коэффициенты) регрессии,
— параметры (коэффициенты) регрессии,  — регрессоры (факторы модели), k — количество факторов модели.
— регрессоры (факторы модели), k — количество факторов модели.
Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):

Параметр 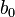 , при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:
, при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:
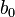 , при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:
, при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу: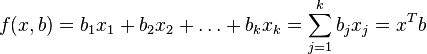 ,
,
где  — вектор регрессоров,
— вектор регрессоров, 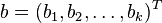 — вектор-столбец параметров (коэффициентов).
— вектор-столбец параметров (коэффициентов).
 — вектор регрессоров,
— вектор регрессоров, 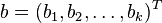 — вектор-столбец параметров (коэффициентов).
— вектор-столбец параметров (коэффициентов).
Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно
Проверка значимости регрессии
Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:
где R - коэффициент корреляции;
f1 и f2 - число степеней свободы.
Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f1 равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f1=1). Число степеней свободы необъясненной дисперсии f2 = N-k-1, где N-количество экспериментальных точек, k-количество объясняющих переменных (например, для модели Y=A*X+B подставляем k=1).
Еще один пример:
для линейной модели вида Y=A0+A1*X1+A2*X2, построенной по 20 экспериментальным точкам, получаем f1=2 (две переменных X1 и X2), f2=20-2-1=17.
Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным, взятым для числа степеней свободы f1 (бóльшая дисперсия) и f2 (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.
Коэффициент корреляции и F-критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих метод наименьших квадратов.
Основы теории проверки статистических гипотез. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия. Примеры.
Основы теории проверки статистических гипотез
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина  , распределение которой
, распределение которой  полностью или частично неизвестно. Тогда любое утверждение, относительно
полностью или частично неизвестно. Тогда любое утверждение, относительно  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
 , распределение которой
, распределение которой  полностью или частично неизвестно. Тогда любое утверждение, относительно
полностью или частично неизвестно. Тогда любое утверждение, относительно  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:- Статистическая гипотеза, однозначно определяющая распределение
 , то есть
, то есть 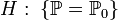 , где
, где  какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.
- Статистическая гипотеза, утверждающая принадлежность распределения
 к некоторому семейству распределений, то есть вида
к некоторому семейству распределений, то есть вида 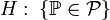 , где
, где 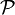 — семейство распределений, называется сложной.
— семейство распределений, называется сложной.
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу  . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей илиальтернативной.
, называемая конкурирующей илиальтернативной.
 . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей илиальтернативной.
, называемая конкурирующей илиальтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на случайной выборке  фиксированного объема
фиксированного объема  для распределения
для распределения  . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной (см. Последовательный статистический критерий).
. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной (см. Последовательный статистический критерий).
 фиксированного объема
фиксированного объема  для распределения
для распределения  . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной (см. Последовательный статистический критерий).
. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной (см. Последовательный статистический критерий).Пример
Пусть дана независимая выборка  из нормального распределения, где
из нормального распределения, где  — неизвестный параметр. Тогда
— неизвестный параметр. Тогда  , где
, где  — фиксированная константа, является простой гипотезой, а конкурирующая с ней
— фиксированная константа, является простой гипотезой, а конкурирующая с ней 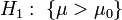 — сложной.
— сложной.
 из нормального распределения, где
из нормального распределения, где  — неизвестный параметр. Тогда
— неизвестный параметр. Тогда  , где
, где  — фиксированная константа, является простой гипотезой, а конкурирующая с ней
— фиксированная константа, является простой гипотезой, а конкурирующая с ней 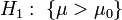 — сложной.
— сложной.Ошибки 1-го и 2-го рода
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие "принять нулевую гипотезу". Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны  ).
).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия | H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) | H0 верно отвергнута | |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называетсямощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Подписаться на:
Комментарии (Atom)












