Иногда вместо термина нормальное распределение употребляют термин гауссовское распределение в честь К. Гаусса (более старые термины, практически не употребляемые в настоящее время: закон Гаусса, Гаусса-Лапласа распределение).
нормальное
Двумерное нормальное распределение
Одномерное нормальное распределение естественно обобщается на двумерное нормальное распределение.
Например, если вы рассматриваете сигнал только в одной точке, то вам достаточно одномерного распределения, в двух точках – двумерного, в трех точках – трехмерного и т.д.
Общая формула для двумерного нормального распределения имеет вид:

 Где
Где  – парная корреляция между X1 и X2;
– парная корреляция между X1 и X2;
 – среднее и стандартное отклонение переменной X1 соответственно;
– среднее и стандартное отклонение переменной X1 соответственно;
 – среднее и стандартное отклонение переменной X2 соответственно.
Если случайные величины Х1 и Х2 независимы, то корреляция равна 0,
– среднее и стандартное отклонение переменной X2 соответственно.
Если случайные величины Х1 и Х2 независимы, то корреляция равна 0,  = 0, соответственно средний член в экспоненте зануляется, и мы имеем:
f(x1,x2) = f(x1)*f(x2)
= 0, соответственно средний член в экспоненте зануляется, и мы имеем:
f(x1,x2) = f(x1)*f(x2)
равномерное
Пример 2.2.8 (двумерное равномерное распределение). Плотность 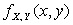 равномерного распределения на области
равномерного распределения на области 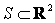 конечной двумерной площади
конечной двумерной площади 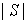 :
: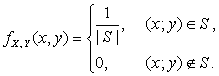
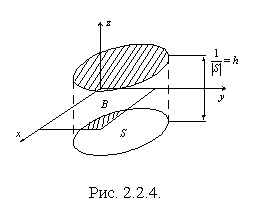 Вероятность
Вероятность 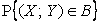 в этом случае определяется отношением площадей
в этом случае определяется отношением площадей 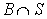 и S (рис. 2.2.4):
и S (рис. 2.2.4):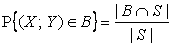 .
.

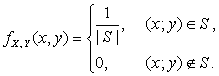
 Вероятность
Вероятность
Комментариев нет:
Отправить комментарий