Задачи теории оценивания. Точечное оценивание. Свойства точечных оценок.
Оценка параметра — соответствующая числовая характеристика, рассчитанная по выборке. Когда оценка определяется одним числом, она называется точечной оценкой.
Свойства точечных оценок[
Оценка 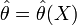 называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
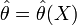 называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности: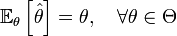 ,
,
где 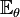 обозначает математическое ожидание в предположении, что
обозначает математическое ожидание в предположении, что 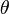 — истинное значение параметра (распределения выборки
— истинное значение параметра (распределения выборки 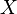 ).
).
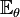 обозначает математическое ожидание в предположении, что
обозначает математическое ожидание в предположении, что 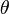 — истинное значение параметра (распределения выборки
— истинное значение параметра (распределения выборки 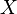 ).
).- Оценка
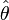 называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок. - Оценка
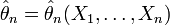 называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:
называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: 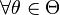 ,
,
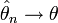 по вероятности при
по вероятности при 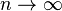 .
.- Оценка
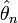 называется сильно состоятельной, если
называется сильно состоятельной, если 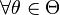 ,
,
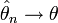 почти наверное при
почти наверное при 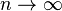 .
.
Надо отметить, что проверить на опыте сходимость «почти наверное» не представляется возможным, поэтому с точки зрения прикладной статистики имеет смысл говорить только о сходимости по вероятности.
Комментариев нет:
Отправить комментарий