Гауссовская (нормальная) случайная величина ее числовые характеристики. Вероятность попадания гауссовской случайной величины в заданный интервал. Правило «трех сигма».

Гауссовская (нормальная) случайная величина ее числовые характеристики. 

Гауссовская случайная величина

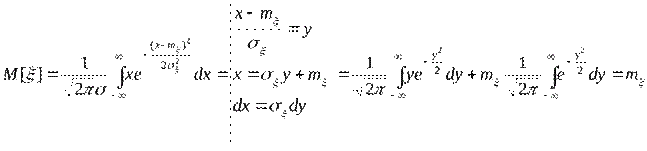
Случайная непрерывная величина X имеет нормальное (гауссово) распределение, если ее плотность распределения вероятности имеет вид

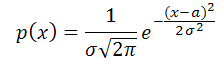
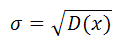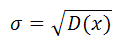где  — среднее квадратическое отклонение; а — математическое ожидание.

Если а=0 и σ=1, то нормальное (гауссовое) распределение называется стандартным нормальным (гауссовым) распределением (таблица плотности вероятности нормальной случайной величины), плотность которого равна

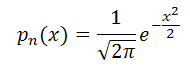
а функция распределения (функция Лапласа) (таблица функции Лапласа)

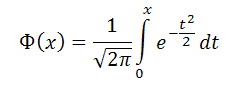
Вероятность попадания гауссовской случайной величины в заданный интервал. 

Вероятность попадания в заданный интервал (α;β) нормально распределенной случайной величины с параметрами а, σ вычисляется по формуле:

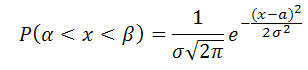
Правило «трех сигма».

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.