Числовые характеристики случайных величин, их свойства
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
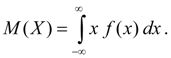 (6б) (6б)
Несобственный интеграл (6б) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М ( Х) не существует). Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
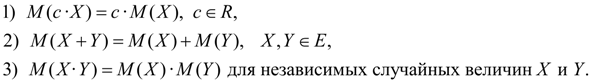 (7) (7)
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
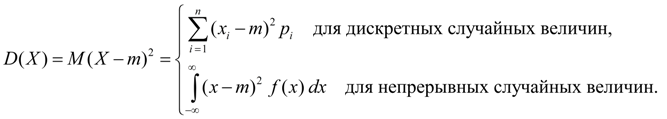 (9) (9)
Здесь m = М ( Х ).
Свойства дисперсии:
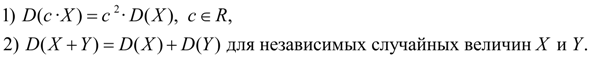 (10) (10)Среднее квадратичное отклонение:
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х0называется математическое ожидание М ( Х – х0)k . Моменты относительно начала координат х = 0 называются начальными моментамии обозначаются:
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).
Теперь очевидно, что дисперсия – это центральный момент второго порядка:
Асимметрия. Центральный момент третьего порядка:
служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерногокоэффициента асимметрии:
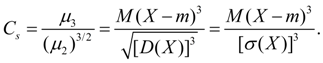 (18) (18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
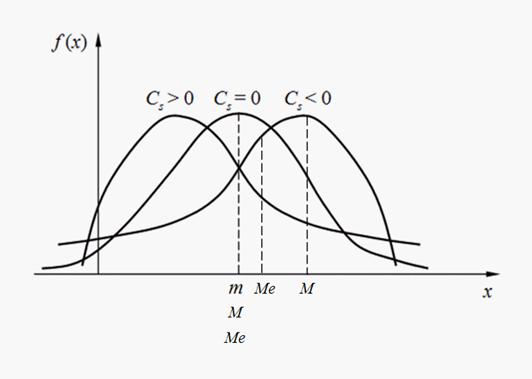 Рис. 2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
служит для оценки так называемого эксцесса, определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения
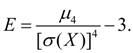 (20) (20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
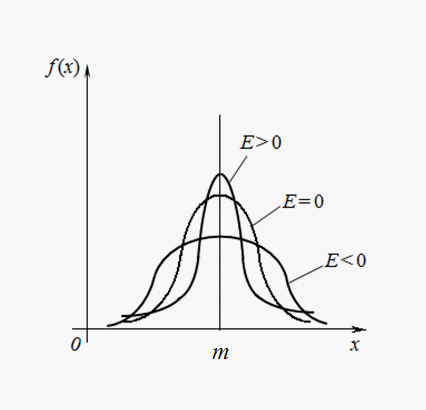 Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство:
|
Комментариев нет:
Отправить комментарий