Независимость нескольких случайных величин.
Случайные величины 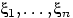 называют независимыми (в совокупности), если для любого набораборелевских множеств
называют независимыми (в совокупности), если для любого набораборелевских множеств 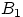 , ...,
, ..., 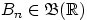 имеет место равенство:
имеет место равенство:
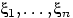 называют независимыми (в совокупности), если для любого набораборелевских множеств
называют независимыми (в совокупности), если для любого набораборелевских множеств 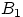 , ...,
, ..., 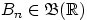 имеет место равенство:
имеет место равенство: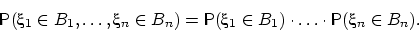
Связь с коэффициентом корреляции.
Коэффициент корреляции - это сила и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между - 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной, а когда значение r отрицательно, связь также отрицательна. Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует.
Условные законы распределения. Примеры.
Условным распределением составляющей X при Y = yj называют совокупность условных вероятностей P(x1½yj), P(x2½yj), …, P(xn½yj), вычисленных в предположении, что событие Y = yj (j имеет одно и то же значение при всех возможных значениях X) уже наступило.
Аналогично определяется условное распределение составляющей Y.
Условный закон распределения X в предположении, что событие
Y = y1 уже произошло, может быть найден по следующей формуле:
Y = y1 уже произошло, может быть найден по следующей формуле:
 . (77)
. (77)
В общем случае условные законы для составляющей X могут быть представлены в виде формуле
 . (78)
. (78)
Для составляющей Y условные законы определяются формулой
 . (79)
. (79)
Пример 3.2. Найти условный закон распределения составляющей X при условии, что составляющая Y приняла значение y1 и двумерная случайная величина (Х, Y) задана таблицей:
 X Y X Y | x1 | x2 | x3 |
| y1 | 0,10 | 0,30 | 0,20 |
| y2 | 0,06 | 0,18 | 0,16 |
Решение. Используя формулу
 ,
,
где P(y1) = 0,10 + 0,30 + 0,20 = 0,60, находим:
 ;
; ;
; .
.
Для проверки вычислений просуммируем найденные вероятности:
 .
.
Искомый условный закон распределения X может быть записан в виде таблицы
| X | x1 | x2 | x3 |
 |  |  |  |
Аналогично найдем условный закон распределения Y, который приведен в виде следующей таблицы:
| Y | y1 | y2 |
 |  |  |
Проверка:  .
.
 .
.
Комментариев нет:
Отправить комментарий