Плотность распределения вероятностей системы двух случайных величин (двумерного случайного вектора), ее свойства. Примеры.
Предположим, что функция распределения 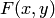 непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции
непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции 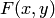
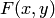 непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции
непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции 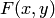
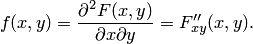
Функция 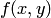 называется плотностью распределения системы непрерывных случайных величин
называется плотностью распределения системы непрерывных случайных величин 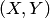 . Зная плотность распределения
. Зная плотность распределения 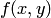 , можно определить вероятность попадания случайной точки
, можно определить вероятность попадания случайной точки 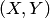 в произвольную область
в произвольную область 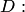
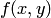 называется плотностью распределения системы непрерывных случайных величин
называется плотностью распределения системы непрерывных случайных величин 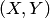 . Зная плотность распределения
. Зная плотность распределения 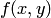 , можно определить вероятность попадания случайной точки
, можно определить вероятность попадания случайной точки 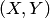 в произвольную область
в произвольную область 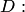
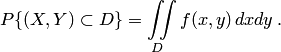
| (5.1) |
Используя формулу (5.1), выразим функцию распределения системы 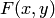 через плотность распределения
через плотность распределения 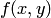 :
:
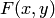 через плотность распределения
через плотность распределения 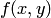 :
: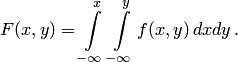
| (5.2) |
Рассмотрим свойства плотности распределения системы двух случайных величин.
Свойство 1. Плотность распределения есть функция неотрицательная: 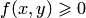 .
.
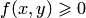 .
.
Свойство 2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице:
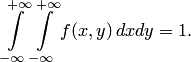
Комментариев нет:
Отправить комментарий