Простая линейная регрессия. Оценки параметров. Проверка значимости регрессии. Примеры.

Простая линейная регрессия. 

Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.

Регрессионная модель

,

где  — параметры модели,  — случайная ошибка модели, называется линейной регрессией, если функция регрессии  имеет вид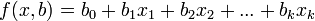

,

где  — параметры (коэффициенты) регрессии,  — регрессоры (факторы модели), k — количество факторов модели.

Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):

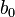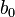Параметр , при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:

,

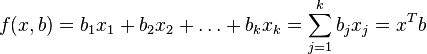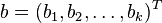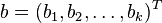где  — вектор регрессоров,  — вектор-столбец параметров (коэффициентов).

Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно

Проверка значимости регрессии

Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:
   
где R - коэффициент корреляции;
      f₁ и f₂ - число степеней свободы.
Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f₁ равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f₁=1). Число степеней свободы необъясненной дисперсии f₂ = N-k-1, где N-количество экспериментальных точек, k-количество объясняющих переменных (например, для модели Y=A*X+B подставляем k=1).
Еще один пример:
для линейной модели вида Y=A₀+A₁*X₁+A₂*X₂, построенной по 20 экспериментальным точкам, получаем f₁=2 (две переменных X₁ и X₂),   f₂=20-2-1=17.
Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным, взятым для числа степеней свободы f₁ (бóльшая дисперсия) и f₂ (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.

Коэффициент корреляции и F-критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих метод наименьших квадратов.