Системы случайных величин.
Упорядоченная пара (X,Y) случайных величин X и Y называется двумерной случайной величиной, или случайным вектором двумерного пространства. Двумерная случайная величина (X,Y) называется также системой случайных величина X и Y. Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины. Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:
P(X=xi, Y=yj) = pij, i=1,2...,n, j=1,2...,m
Пусть Х = (Х1, Х2,…,ХN) – cовокупность (или система) случайных величин.
Функция распределения вероятностей системы двух случайных величин (двумерного случайного вектора), се свойства
Функцией распределения системы случайных величин называется вероятность совместного выполнения неравенств 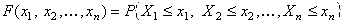 ,
, 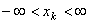 , K = 1, 2, ..., N.
, K = 1, 2, ..., N.
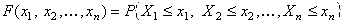 ,
, 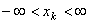 , K = 1, 2, ..., N.
, K = 1, 2, ..., N.
Свойства функции распределения аналогичны свойствам функции распределения одномерной случайной величины. Например, для системы двух случайных величин X и Y:
1) F(х, у) – неубывающая функция своих аргументов;
2) 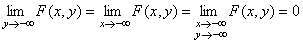 ;
;
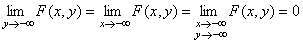 ;
;
3) 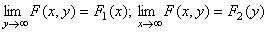 , где F1(X), F2(Y) – функции распределения компонент X и Y;
, где F1(X), F2(Y) – функции распределения компонент X и Y;
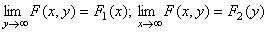 , где F1(X), F2(Y) – функции распределения компонент X и Y;
, где F1(X), F2(Y) – функции распределения компонент X и Y;
4) 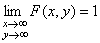 .
.
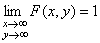 .
.
Комментариев нет:
Отправить комментарий