Описательная статистика. Эмпирическая функция распределения. Гистограмма, полигон частот. Статистический ряд, группировка значений выборки. Выборочные числовые характеристики. Примеры.

Описательная статистика.

Описательная статистика используется для простого обобщения данных, полученных в рамках выборочного исследования. В свою очередь, статистические выводы необходимы для того, чтобы данные, полученные из выборки, можно было распространить на всю генеральную совокупность.

Эмпирическая функция распределения.

Эмпирической функцией выборки (функцией распределения выборки) называется функция

Fn(x)=	nx
	n

, которую можно записать в следующем виде:

 

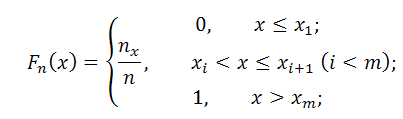
  Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке х_i, где х_i — варианта рассматриваемого статистического распределения. 

  Пример

  По заданной выборке построить эмпирическую функцию выборки. 

хi	2	4	5	6	7
ni	5	3	4	5	3

F20(X≤2)=	0	=0
	20

F20(4)=	5	=0.25
	20

F20(5)=	5+3	=0.4
	20

F20(6)=	5+3+4	=0.6
	20

F20(7)=	5+3+4 +5	=0.85
	20

F20(X>7)=	5+3+4 +5 +3	=1
	20

 

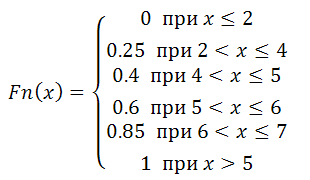
  График данной функции представлен ниже:

 

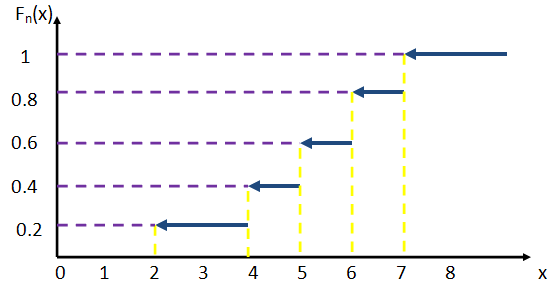
Гистограмма, полигон частот.

Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i;n_i) соединяют отрезками прямых и получают полигон частот (Рис. 1).

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x₁; W₁), (x₂; W₂), ..., (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им относительные частоты W_i. Точки ( x_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i / h.

Площадь i - го частичного прямоугольника равна hn_i / h = n_i - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению W_i / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i / h (Рис. 2).

Площадь i - го частичного прямоугольника равна hW_i / h = W_i - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Рис. 1. Полигон частот

Рис. 2. Гистограмма относительных частот

Статистический ряд, группировка значений выборки.

Статистический ряд распределения - это упорядоченое распределение единиц совокупности на группы по определенному варьирующему признаку.

Выборочные числовые характеристики. 

Следующим этапом обработки данных является вычисления числовых характеристик выборки. Главные из них:среднее значение, дисперсия, среднее квадратическое значение, моменты.
Так как функцию выборочных значений называют статистикой, то числовые характеристики, вычисленные по выборке, также называют статистиками.
Числовые характеристики, вычисленные по генеральной совокупности, называют параметрами генеральной совокупности.

7.1 Выборочное среднее

Для конкретной выборки объема n ее выборочное среднее  определяется соотношением

где хi – значение элемента выборки.
Обычно требуется описать статистические свойства произвольных случайных выборок одного объема, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как независимые случайные величины Хi, принимающие значения хi с одной и тоже плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной , равной

Среднее значение генеральной совокупности, из которой производится выборка, будем называть генеральным средним и обозначать mх. При значительном объеме выборки можно ожидать, что выборочное среднее не будет заметно отличаться от генерального среднего. Поскольку выборочное среднее является случайной величиной, то для нее можно найти математическое ожидание:

Таким образом, математическое ожидание выборочного среднего равно генеральному среднему. В этом случае говорят, что выборочное среднее является несмещенной оценкой генерального среднего. В дальнейшем мы вернемся к этому термину. Так как выборочное среднее является случайной величиной, флуктуирующей вокруг генерального среднего, то желательно оценить эту флуктуацию с помощью дисперсии выборочного среднего. Рассмотрим выборку, объем которой n значительно меньше объема генеральной совокупности N (n << N). Предположим, что при формировании выборки характеристики генеральной совокупности не меняются, что эквивалентно предположению N = ¥. Тогда

Случайные величины Хi и Xj (i¹j) независимы, следовательно,

Подставим полученный результат в формулу для дисперсии:
, где – дисперсия генеральной совокупности. Тогда среднее квадратическое отклонение выборочного среднего  равно:
.
Из этой формулы следует, что с увеличением объема выборки флуктуации среднего выборочного около среднего генерального уменьшаются как . Проиллюстрируем сказанное примером. Пусть имеется случайный сигнал с математическим ожиданием и дисперсией, соответственно равными mx = 10,  = 9.
Отсчеты сигнала берутся в равноотстоящие моменты времени t1, t2, ... , tn.



Так как отсчеты являются случайными величинами, то будем их обозначать X(t1), X(t2), ... , X(tn).
Определим количество отсчетов, чтобы среднее квадратическое отклонение оценки математического ожидания сигнала не превысило 1% его математического ожидания. Поскольку mx=10, то нужно, чтобы  С другой стороны  поэтому  или Отсюда получаем, что n ³ 900 отсчетов.

7.2. Выборочная дисперсия

По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой (приближенным значением) генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии. Выборочная дисперсия  для выборки, состоящей из случайных величин , определяется следующим образом:

Используя это представление выборочной дисперсии, найдем ее математическое ожидание




Таким образом, мы получили, что . Это значит, что выборочная дисперсия является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку, нужно величину умножить на  тогда и выборочная дисперсия  принимает вид:
=
Итак, мы получили следующий результат. Если в результате n независимых измерений случайной величины Хс неизвестным математическим ожиданием и дисперсией нам нужно по полученным данным определить эти параметры, то следует пользоваться такими оценками:

В случае, если известно математическое ожидание генеральной совокупности mx, то выборочную дисперсию следует вычислять по формуле
=
которая также является несмещенной оценкой.
Относительной оценкой степени разброса случайной величины Х по отношению к выборочному среднему является коэффициент вариации Vстатистического распределения выборки:
.
Часто по выборочным данным нужно знать оценки таких параметров генеральной совокупности как:центрального (начального) момента k – го порядка, коэффициента асимметрии As, эксцесса Ех. 
Выборочным центральным (начальным) моментом k – го порядка  ()называют величину
()
Для оценки отклонения статистического распределения выборки от нормального распределения используют числовые характеристики - выборочный коэффициент асимметрии  и выборочный эксцесс.
Выборочным коэффициентом называют число, которое вычисляется по формуле:
.
Выборочным эксцессом статистического распределения называют число
.
Заметим, что представленные формулы записаны с использованием статистического ряда. В случае интервального вариационного ряда эти формулы преобразуются путем введения весов, равных частоте появления варианты хj. Эти характеристики называются взвешенными числовыми характеристиками. Таквзвешенный центральный (начальный) момент k – го порядка будет иметь вид:
 (),
где nj – частота варианты xj ()