Независимые испытания Бернулли.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события в единичном испытании буквой , т.е. , а вероятность противоположного события (событие не наступило) - буквой .
Формула Бернулли.
Распределение числа успехов (появлений события) носит название биномиального распределения.
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности
 ,
,  .
.
По формуле Бернулли требуемая вероятность равна
 .
.
 ,
,  .
.По формуле Бернулли требуемая вероятность равна
 .
.Наивероятнейшее число успехов.
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов  (появлений события) имеет вид:
(появлений события) имеет вид:
 (появлений события) имеет вид:
(появлений события) имеет вид:
Так как  , то эти границы отличаются на 1. Поэтому
, то эти границы отличаются на 1. Поэтому  , являющееся целым числом, может принимать либо одно значение, когда
, являющееся целым числом, может принимать либо одно значение, когда  целое число (
целое число ( ) , то есть когда
) , то есть когда  (а отсюда и
(а отсюда и  ) нецелое число, либо два значения, когда
) нецелое число, либо два значения, когда  целое число.
целое число.
 , то эти границы отличаются на 1. Поэтому
, то эти границы отличаются на 1. Поэтому  , являющееся целым числом, может принимать либо одно значение, когда
, являющееся целым числом, может принимать либо одно значение, когда  целое число (
целое число ( ) , то есть когда
) , то есть когда  (а отсюда и
(а отсюда и  ) нецелое число, либо два значения, когда
) нецелое число, либо два значения, когда  целое число.
целое число.
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.

Следовательно,  .
.
 .
.Полиномиальная схема.
Рассмотрим опыт, состоящий в n-кратном повторении одинаковых независимых испытаний, в каждом может произойти одно и только одно из m несовместных событий А1, А2, …, Аm, причем каждое событие Аi может произойти с вероятностью рi. Такой опыт называют полиномиальной (мультиноминальной) схемой.
Вероятность того, что в n испытаниях событие А1 произойдет равно k1 раз, событие А2 произойдет равно k2 раз, …, событие Аm произойдет равно km раз (причем k1 + k2 + … + km = n) равна
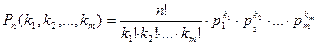 (1.38)
(1.38)
Пример 1.66. В некотором государстве живут 60% блондинов, 25% брюнетов и 15% шатенов. Найдем вероятность того, что среди восьми наугад отобранных подданных этого государства окажутся четыре блондина, три брюнета и один шатен.
В данном случае мы имеем дело с полиномиальной схемой, в которой m=3; p1=0,6; p2=0,25; p3=0,15; n=8; k1=4; k2=3; k3=1.
Согласно формуле (1.38) искомая вероятность равна
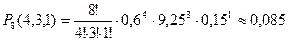


Комментариев нет:
Отправить комментарий