6) Гиперболические функции и их свойства.

sh x - гиперболический синус

,     –∞ < x < +∞;   –∞ < y < +∞.

ch x - гиперболический косинус

,     –∞ < x < +∞;   1 ≤ y < +∞.

th x - гиперболический тангенс

,     –∞ < x < +∞;   – 1 < y < +1.

cth x - гиперболический котангенс

,     x ≠ 0;   y < –1   или   y > +1.

Графики гиперболических функций

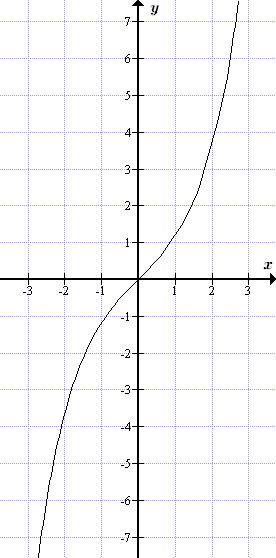
График гиперболического синуса  y = sh x

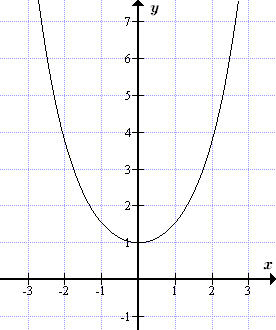
График гиперболического косинуса  y = ch x

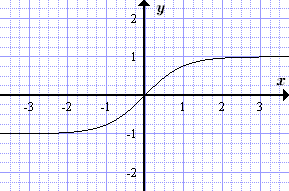
График гиперболического тангенса  y = th x

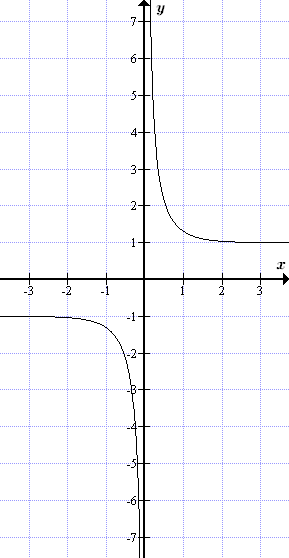
График гиперболического котангенса  y = cth x

Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ;     cos iz = ch z
sh iz = i sin z ;     ch iz = cos z
tg iz = i th z ;     ctg iz = – i cth z
th iz = i tg z ;     cth iz = – i ctg z
Здесь   i – мнимая единица,   i² = –1.

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh(–x) = – sh x;   ch(–x) = ch x.
th(–x) = – th x;   cth(–x) = – cth x.

Функция   ch(x)   – четная. Функции   sh(x),   th(x),   cth(x) – нечетные.

Разность квадратов

ch² x – sh² x = 1.