Угол между прямой и плоскостью.

Определение.

 Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Формула вычисления угла между прямой и плоскостью

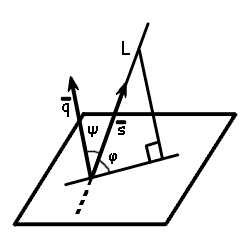
Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	| A · l + B · m + C · n |
	√A2 + B2 + C2 · √l2 + m2 + n2

Вывод формулы для вычисления угла между прямой и плоскостью

Из уравнения прямой можно найти направляющий вектор прямой

s = {l; m; n}

Из уравнения плоскости вектор нормали плоскости имеет вид

q = {A; B; C}

Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой

cos ψ =	| q · s |
	| s | · |q |

Так как φ = 90° - ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.

Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.