Квадратичная форма.
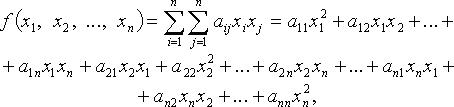
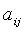 - коэффициенты квадратичной формы. Без ограничения общности считают
- коэффициенты квадратичной формы. Без ограничения общности считают 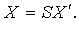 тогда
тогда
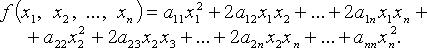
Приведение квадратичной формы к каноническому виду.
 , а через
, а через  обозначены все остальные слагаемые.
обозначены все остальные слагаемые.
 представляет собой квадратичную форму от n-1 переменных
представляет собой квадратичную форму от n-1 переменных 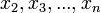 .
.
Квадратичная форма переменных 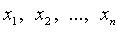 - функция
- функция
Если переменные 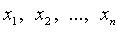 принимают действительные значения и
принимают действительные значения и 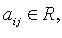 квадратичная форма называется действительной.
квадратичная форма называется действительной.
Приведение квадратичной формы к каноническому виду.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть задана квадратичная форма:
В силу симметричности матрицы 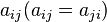 квадратичную форму можно переписать следующим образом:
квадратичную форму можно переписать следующим образом:
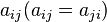 квадратичную форму можно переписать следующим образом:
квадратичную форму можно переписать следующим образом:
Возможны два случая:
- хотя бы один из коэффициентов
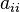 при квадратах отличен от нуля. Не нарушая общности, будем считать
при квадратах отличен от нуля. Не нарушая общности, будем считать  (этого всегда можно добиться соответствующей перенумерацией переменных);
(этого всегда можно добиться соответствующей перенумерацией переменных); - все коэффициенты
 , но есть коэффициент
, но есть коэффициент  , отличный от нуля (для определённости пусть будет
, отличный от нуля (для определённости пусть будет  ).
).
В первом случае преобразуем квадратичную форму следующим образом:
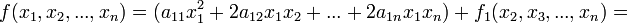

 , где
, где
 , а через
, а через  обозначены все остальные слагаемые.
обозначены все остальные слагаемые. представляет собой квадратичную форму от n-1 переменных
представляет собой квадратичную форму от n-1 переменных 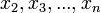 .
.
С ней поступают аналогичным образом и так далее.
Заметим, что 

Второй случай заменой переменных  сводится к первому.
сводится к первому.
 сводится к первому.
сводится к первому.
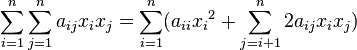
Комментариев нет:
Отправить комментарий