Линейный оператор. Матрица линейного оператора

Линейный оператор. 

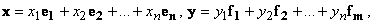
Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.

Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.

Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.

Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:

A(u + v) = A(u ) + A(v) ,  A(α·u) = α· A(u).

Матрица линейного оператора

Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .

В этих пространствах определены базисы e = {e₁, ..., e_n} и f = {f₁, ..., f_m}.

Пусть A(e_i ) = a_1i·f₁ + a_2i·f₂ + ...+ a_mi·f_m — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n.

Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {a_ij}= {A(e_j )_i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:

y = A· x,