Условие параллельности и перпендикулярности двух прямых.
Если уравнения прямой заданы в общем виде
A1x + B1y + C1 = 0,
A2x + B2y + C2 = 0, (6)
угол между ними определяется по формуле
4. Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2. (8)
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
Условие перпендикулярности двух прямых
Условием перпендикулярности двух прямых, заданных уравнениями
служит соотношение
т.е. две прямые перпендикулярны, если произведение их угловых коэффициентов равно -1, и не перпендикулярны, если оно не равно -1.
Пример 1.
Прямые
перпендикулярны, так как
Пример 2.
Прямые
не перпендикулярны, так как
Условие перпендикулярности двух прямых через определитель
Если две прямые представлены уравнениями
| 7. |
|
A1 x+ B1 y+ C1= 0
A1 x+ B1 y+ C1= 0
|
|
то условие их перпендикулярности есть
Пример 3.
Прямые
перпендикулярны. Здесь
| 11. |
А1= 2, А2= 5, В1= 5, В2=−2,
|
значит,
| 12. |
А1 А2+ В1 В2= 10 – 10= 0
|
Пример 4.
Прямые
не перпендикулярны, так как здесь
Угол между прямыми.
Пусть две неперпендикулярные прямые L1, L2 (взятые в данном порядке) представляются уравнениями
Тогда угол между двумя прямыми найдется по формуле
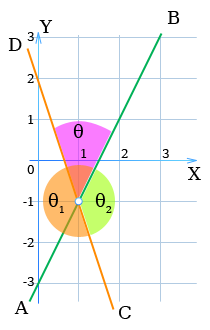
Угол между двумя прямыми
то выражение стоящее в знаменателе, обращается в нуль
и частное перестает существовать. Одновременно перестает существовать («обращается в бесконечность») tg(θ). Формула (2), понимаемая буквально, теряет смысл, но в этом случае ее нужно понимать условно. Именно, всякий раз, как в знаменателе появляется нуль, угол θ надо считать равным ±90° (как поворот на +90°, так и поворот на -90° совмещает любую из перпендикулярных прямых с другой).
то формула (2) вовсе неприменима, ибо тогда одну из прямых (или обе) нельзя представить уравнением вида (1).
В этом случае угол θ определяется следующим образом:
а) когда прямая L2 параллельная оси OY, а L1 не параллельна, применяем формулу
б) когда прямая L1 параллельна оси OY, а L2 не параллельна, применяем формулу
в) когда обе прямые параллельны оси OY, они параллельны и между собой, так что
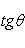
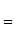
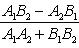
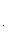 (7)
(7)
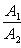
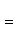
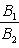
 (9)
(9)


Комментариев нет:
Отправить комментарий